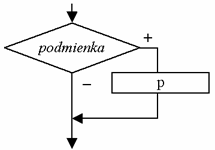
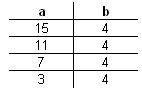Vetvenie je v algoritmizácii reprezentované podmienkou, ktorá predstavuje možnosť rozhodnúť sa podľa pravdivosti skúmaného znaku. V závislosti od jej splnenia sa postup vetví na rôzne prípady. Ak je podmienka splnená, pokračuje sa vykonávaním vetvy označenej ako „+“ , v opačnom prípade sa spracúvajú príkazy vo vetve „-“.
Vetvenie, v ktorom sa príkazy vykonávajú ako v kladnej, tak i v zápornej vetve sa označuje ako úplné.
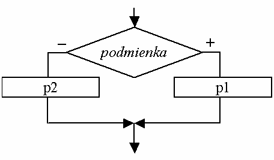
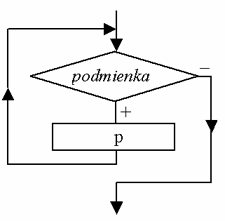
No často sa môžeme stretnúť i so stavom, že príkazy sú uvedené len v prípade splnenia či nesplnenia podmienky. Takéto vetvenie sa označuje ako neúplné, no neznamená to, že je menejcenné – veľmi často totiž nie je potrebné niektoré príkazy pri splnení podmienky vykonávať.

Napíšte algortimus na nájdenie maxima z dvoch čísel.
{VST: a,b – ľubovoľné čísla}
?
{VÝS: max – maximum z dvojice}
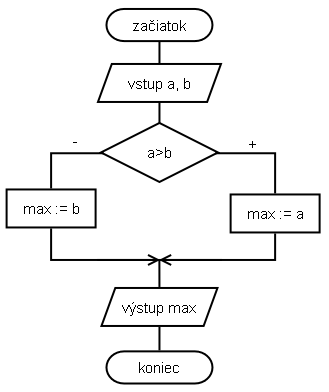
- zo vstupu prečítame dvojicu čísel,
- ak a>b, algoritmus pokračuje vykonávaním príkazov vo vetve „+“ a je jasné, že maximom z dvojice je a. V opačnom prípade môže byť a<b alebo sú obe čísla rovné. Tak či onak, správnou hodnotou bude hodnota uložená v premennej b.
- premennú max, do ktorej sme výsledok ukladali, len vypíšeme.
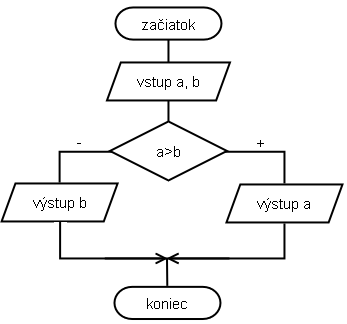
Algoritmus by sme mohli vytvoriť i jednoduchým výpisom hodnoty bez použitia ďalšej premennej.
{VST: a,b – ľubovoľné čísla}
?
{VÝS: maximum z dvojice}

Napíšte algoritmus na zistenie podielu dvoch čísel.
Zistiť podiel znamená vydeliť dve čísla. Mohli by sme prečítať čísla, priradiť ich podiel do premennej a vypísať ho, ale môže nastať prípad, že ako deliteľa zadáme nulu. A už v prvej triede na základnej škole nás učili, že nulou deliť nemožno. Preto potrebujeme takúto situáciu ošetriť – v prípade zadania nuly sa vypíše text „Nulou nedelíme!“, inak sa vypočíta podiel a vypíše sa.
{VST: a,b – ľubovoľné čísla}
?
{VÝS: podiel – podiel dvojice}
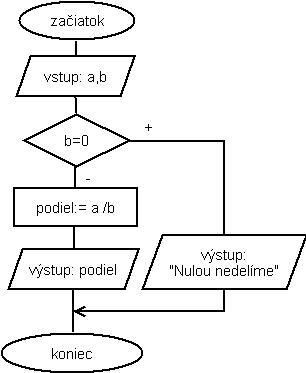
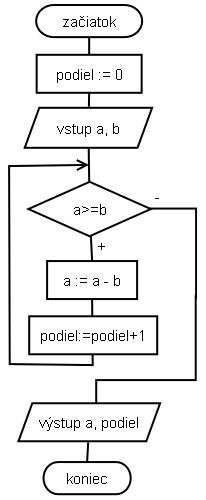
- prečítame dvojicu čísel
- ak je druhé číslo nula, vypíšeme upozornenie
- ak je b nenulové, vypočítame podiel a vypíšeme ho
Pokiaľ je text za príkazom výstup v úvodzovkách, vypíše sa presne to, čo je v úvodzovkách. Ak text za výstupv úvodzovkách nie je, považuje sa za premennú.
Ak potrebujeme vetviť postup na viacero rôznych riešení v závislosti od podmienky, vkladáme viacero alternatív “do seba”.

Napíšte algortimus na nájdenie maxima z dvoch čísel a v prípade, že sú rovnaké, podajte o tom informáciu.
{VST: a,b – ľubovoľné čísla}
?
{VÝS: maximum z dvojice alebo info o rovnosti}
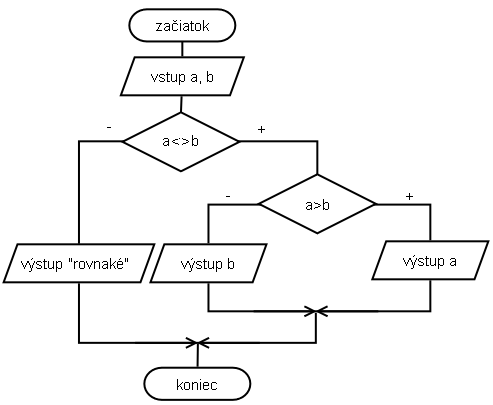
- zo vstupu prečítame dvojicu čísel,
- ak a>b, vypíšeme hodnotu a.
- v opačnom prípade potrebujeme odlíšiť situácie, keď sú čísla rovné a keď a<b. Vložíme do tejto vetvy podmienku a=b, ktorá v prípade kladného výsledku vypíše správu o tom, že hodnoty sú totožné.
- ak neplatí, že a=b, tak je väčším číslom b, pretože v celej tejto vetve platí, že a nie je väčšie ako b a v tomto prípade ani nie sú rovné.

Napíšte algoritmus na nájdenie maxima z troch čísel.
Prvé riešenie by mohlo vyzerať nasledovne:
{VST: a,b,c – ľubovoľné čísla}
?
{VÝS: maximum z trojice}
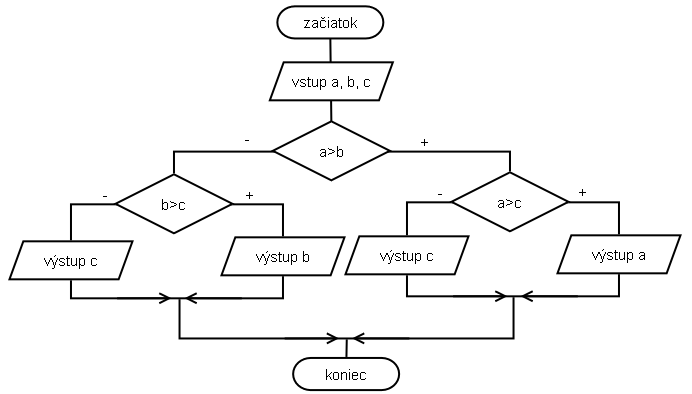
Ak sa však zamyslíme nad energiou, ktorú sme museli venovať uvedomeniu si situácie v jednotlivých vetvách, určite uprednostníme nasledujúce, na prvý pohľad možno dlhšie, no na rozmýsľanie i na možnosť vyvarovať sa chyby určite vhodnejšie riešenie.
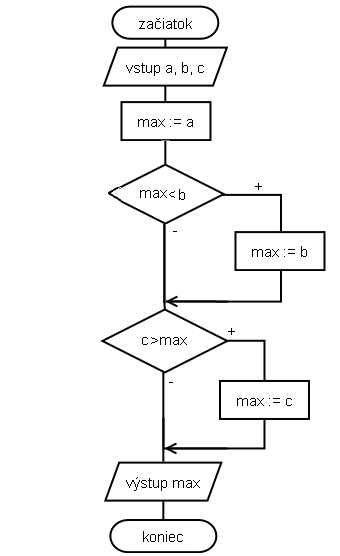
- ako maximum určíme prvé číslo
- ak je b väčšie ako max, tak je jasné, že maximom bude b. V opačnom prípade netreba urobiť nič, v max zostane priradená hodnota a
- ak je hodnota v c väčšia ako hodnota v max (čo môže byť a alebo b), zmeníme ju, inak sa opäť nič nedeje
- vypíšeme max
Záver: nie vždy platí, že najkratšie alebo na prvý pohľad zrejmé riešenie je najvhodnejšie.
Napíšte algoritmus na zistenie absolútnej hodnoty zadaného čísla.
Opäť ide o jednoduchý príklad s neúplným vetvením – ako relatívne nový prvok si dovolíme použiť tú istú premennú na načítanie hodnoty i výpis výsledku.
{VST: a – ľubovoľné čísla}
?
{VÝS: absolútna hodnota z a}
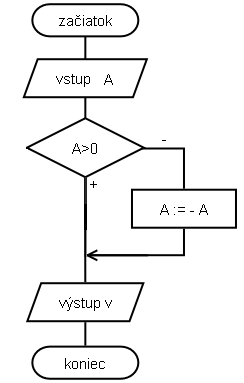
- načítame číslo do premennej a
- ak je a záporné, priradíme doň číslo k nemu opačné, t.j. –a (ako príklad môže slúžiť –5: a:= - -5 = +5)
- v prípade, že a je kladné, nie je potrebné vykonávať nič
- na záver hodnotu vypíšeme
Zložitejšie podmienky
Podmienka je v programovacích jazykoch chápaná ako logický výraz, t. j. zistenie vzťahov (relácie) medzi výrazmi, prípadne zviazané logickými operáciami (and = “a súčasne”, or = “alebo” a not = “neplatí, že”).