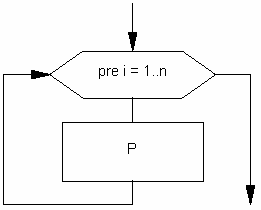
Predpokladom využitia takéhoto cyklu je, že počet opakovaní poznáme pred jeho odštartovaním a operácie v tele naň nemajú žiaden vplyv. Vo všeobecnosti ho možno zapísať:
Napíšte algoritmus na zistenie súčtu prvých 100 čísel.
V tomto prípade budeme pripočítavať čísla po jednom.
Vstup do algoritmu nepotrebujeme, napíšeme ho neuniverzálne tak, že vždy sčíta len prvých 100 čísel. Využijeme cyklus, ktorého počet opakovaní poznáme (100). Každý cyklus so známym počtom opakovaní musí používať premennú – hovorí sa jej riadiaca premenná – ktorá si „pamätá“ koľkokrát cyklus prebehol. V zápise cyklu určíme jej spodnú a hornú hranicu (pre i od 1 po 100). Po skončení tela cyklu sa automaticky (má to na starosti cyklus, nie my) pripočíta hodnota 1 a skočí sa na začiatok cyklu. Zvyšovanie o 1 je štandardné pre všetky cykly so známym počtom opakovaní.
Riadiacu premennú môžeme v tele cyklu používať ako hociktorú inú, neodporúča sa však priraďovať do nej hodnoty (mohlo by sa stať, že cyklus skončí skôr ako predpokladáme, alebo bude nekonečný ak riadiaca paremenná nedosiahne hornú hranicu cyklu).
{VST: }
?
{VÝS: súčet prvých 100 čísel}
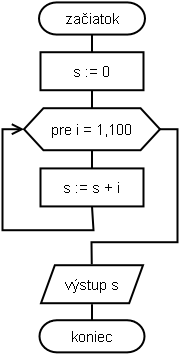
- v prvom riadku vykonáme inicializáciu premennej sucet – priradíme jej počiatočnú hodnotu (niekedy sa stáva, že neinicializovaná premenná obsahuje náhodnú hodnotu, ktorá by „pokazila“ výsledok). V našom prípade je vhodná 0, pretože v nej na začiatku nemá byť umiestnené nič.
- „podmienka“ cyklu zabezpečujúca nastavenie dolnej hranice do riadiacej premennej i, jej zvyšovanie a ukončenie cyklu po dosiahnutí hornej hranice.
- zvýšenie premennej sucet o hodnotu aktuálne uloženú v premennej i. Do premennej sucet sa v každom opakovaní cyklu pridá hodnota uložená v i tak, že sa k premennej sucet pripočíta hodnota i a získaná nová hodnota sa opäť umiestni do premennej sucet.
- ukončenie tela cyklu a zabezpečenie návratu na jeho začiatok,
Na sledovanie hodnôt premenných a overovanie správnosti algoritmu sa často používajú sledovacie tabuľky, prostredníctvom ktorých sa nám často podarí pochopiť činnosť algoritmu oveľa jednoduchšie ako siahodlhým slovným vysvetľovaním.
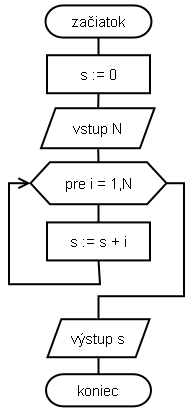
Upravte algoritmus tak, aby bolo možné zadať počet čísel, ktoré sa majú sčítať (na začiatku prečítajte napr. n a nahraďte ním číslo 100 v cykle).
Napíšte algoritmus na zistenie súčinu celých čísel nachádzajúcich sa medzi dvoma zadanými hodnotami, čiže napr. pre hodnoty 5 a 7 bude výsledkom 5*6*7.
{VST: a,b – celé čísla, pre ktoré platí a<b}
?
{VÝS: súčin prvých 100 čísel}
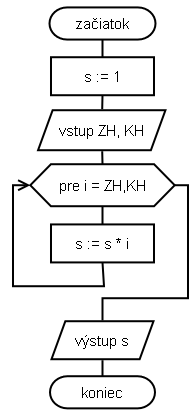
- algoritmus prečíta vstupné hodnoty
- nastaví premennú sucin na hodnotu 1, ktorá v prípade násobenia predstavuje neutrálnu hodnotu (číslo vynásobené 1 sa nezmení). Pokiaľ by sme premennú inicializovali na 0, nedokázali by sme jej hodnotu násobením zmeniť.
- definujeme cyklus od počiatočnej po konečnú hodnotu
- a každou z hodnôt, ktoré bude postupne nadobúdať riadiaca premenná cyklu i, sucin vynásobíme.
- výsledok vypíšeme
Sledovacia tabuľka:
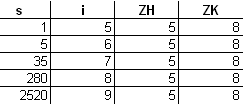
Prostredníctvom cyklu so známym počtom opakovaní (prípadne v kombinácii s príkazmi na okamžité ukončenie cyklu) dokážeme vyriešiť všetky problémy, no niekedy je pohodlnejšie, prehľadnejšie a najmä v súlade zo zásadami štuktúrovaného programovania, použitie ďalších dvoch typov cyklov. Tieto využívame vtedy, keď nám počet opakovaní nie je známy v momente vstupu do cyklu a/alebo ukončenie cyklu ovplyvňujú operácie v jeho tele. Kontrolu ukončenia cyklu môžeme realizovať:
- pred vykonaním kroku (tela) cyklu – cyklus s podmienkou na začiatku
- po vykonaní tela cyklu – cyklus s podmienkou na konci
1. Napíšte algoritmus na zistenie súčinu dvoch celých čísel pre zariadenie, ktoré nepozná operáciu násobenia (nahraďte ju kombináciou cyklu a sčítania).